Зависимость давления и плотности насыщенного водяного пара от температуры.

Функции операционной системы

Программное обеспечение ПО.

Второй этап работы.

У меня на компьютере нету основных программ что бы выполнить задание поэтому я ниписал.

Задачи на равновесие

Задача 1

На балке длиной 4 метра, которая лежит на двух опорах, находятся 2 человека массами m₁=80 кг и m₂=20 кг. Определить силы, действующие на балку.

Дано:

m₁=80кг

m₂=20кг

Найти: N₁; N₂

Решение:

По II закону равновесия ∑M=0

Mm₁g+ Mm₂g+MN₁+ MN₂=0

Точка O: m₁gL₁+ m₂gL₂- N₂L₃=0

L₁=1,125м; L₂=2,125м; L₃=3,25м

m₁gL₁+ m₂gL₂= N₂L₃

N₂= (m₁gL₁+ m₂gL₂)/ L₃

N₂=(80кг*10Н/м*1,125м + 20кг*10Н/м*2,125м)/3,25м

N₂=653Н

По I закону равновесия ∑F=0

-m₁g- m₂g+N₁+ N₂=0

N₁= m₁g+ m₂g- N₂

N₁=80кг*10Н/м+20кг*10Н/м-653Н

N₁=447Н

Ответ: N₂=653Н, N₁=447

Определить массу объекта Х, если силы реакции опор равны 70H и 10Н.

Дано:

N₁=50H

N₂=20H

Найти: m

Решение:

По II Закону равновесия ∑M=0

M N₁ +M N₂ +Mmg=0

Точка О: N₁ L₁-N₂L₂ -mgL₃=0

N₁ L₁-N₂L₂ =m₁gL₃

m= (N₁ L₁-N₂L₂)/(gL₃)

L₁=1,625м; L₂=1,625м; L₃=1м

m= (70Н*1,625м-10Н*1,625м)/(10Н/М*1м)

m=9,75 кг

Ответ: m=9,75 кг

Дано:

m₁=30кг

m₂=60кг

Найти: О

Решение:

По закону равновесия для рычага F₁L₁=F₂L₂

F₁= m₁g

F₂= m₂g

m₁g L₁= m₂g L₂

m₁L₁= m₂L₂

m₁L₁= m₂(L₀- L₁)

m₁L₁= m₂L₀- m₂L₁

m₁L₁ +m₂L₁= m₂L₀

 L₁(m₁+ m₂)= m₂L₀

L₁=(m₁+ m₂)/(m₂L₀)

L₁=(30кг+60кг)/(60кг*3,5м)

L₁≈0,4м

Ответ: на расстоянии 0,4м от края

Кинематика Контроль знаний №1

Задание №1
А.5.5
B.4.3
C.1.1
D.2.4
E.3.1


Задание №2
А.5
Б.2
В.1
Г.4
Д.3

Задание №3
А.2
Б.5
В.1
Г.3
Д.4

Калориметр

 Калори́метр  — прибор для измерения количества теплоты, выделяющейся или поглощающейся в каком-либо физическом, химическом или биологическом процессе. Термин «калориметр» был предложен А. Лавуазье и П. Лапласом (1780).

 Современные калориметры
Современные калориметры работают в диапазоне температур от 0,1 до 3500 К и позволяют измерять количество теплоты с точностью до 0,01-10 %. Устройство калориметров весьма разнообразно и определяется характером и продолжительностью изучаемого процесса, областью температур, при которых производятся измерения, количеством измеряемой теплоты и требуемой точностью.

 Типы калориметров

Калориметр, предназначенный для измерения суммарного количества теплоты Q, выделяющейся в процессе от его начала до завершения, называют калориметр-интегратором; Калориметр для измерения тепловой мощности (скорости тепловыделения) L и её изменения на разных стадиях процесса — измерителем мощности или калориметр-осциллографом. По конструкции калориметрической системы и методу измерения различают жидкостные и массивные калориметры, одинарные и двойные (дифференциальные).

 Жидкостный калориметр-интегратор

Жидкостный калориметр-интегратор переменной температуры с изотермической оболочкой применяют для измерений теплот растворения и теплот химических реакций. Он состоит из сосуда с жидкостью (обычно водой), в котором находятся: камера для проведения исследуемого процесса («калориметрическая бомба»), мешалка, нагреватель и термометр. Теплота, выделившаяся в камере, распределяется затем между камерой, жидкостью и другими частями калориметра, совокупность которых называют калориметрической системой прибора.
У жидкостных калориметров изотермическую температуру оболочки поддерживают постоянной. При определении теплоты химической реакции наибольшие затруднения часто связаны не с учётом побочных процессов, а с определением полноты протекания реакции и с необходимостью учитывать несколько реакций.

задание 3

Задание 1

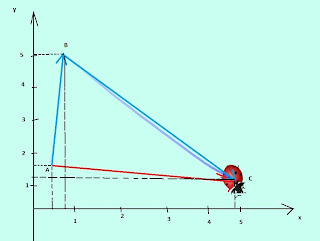
Божья коровка

Цель: Определение координат тела и определение перемещения

1 

1)ДАНО:A(0,5;1,5),B(1;5),C(5;1)
1) AB:
Sx=5-1,5=3,5
Sy=1-1,5=-0,5
[AB]=(3,5^2)+(-0,5^2)- под корнем
[AB]=3,5
2)BC:
Sx=5-1=4
Sy=1-5=4
[BC]=(4^2)+(4^2)- под корнем
[BC]=5,6
3)l=[AB]+[BC]=3,5+5,6=9,1
4)AC:
Sx=5-0,5=4,5
Sy=1-1,5=-0,5
[AC]=(4,5^2)+(-0,5^2)- под корнем
[AC]=4,5 (перемещение)
5)l=9,1
S=4,5

2

2)ДАНО:A(5;1),B(7;4),C(1;5)
1) AB:
Sx=7-5=2
Sy=4-1=3
[AB]=(2^2)+(3^2)- под корнем
[AB]=3,6
2)BC:
Sx=1-7=-6
Sy=5-4=1
[BC]=(-6^2)+(1^2)- под корнем
[BC]=6
3)l=[AB]+[BC]=9,6
4)AC:
Sx=5-1=4
Sy=1-5=-4
[AC]=(4^2)+(-4^2)- под корнем
[AC]=5,6(перемещение)
5)l=9,6
S=5,6

3

3)ДАНО:A(0,5;7,5),B(6;3),C(1;1)
1) AB:
Sx=6-0,5=5,5
Sy=3-7,5=-4,5
[AB]=(5,5^2)+(-4,5^2)- под корнем
[AB]=7,1
2)BC:
Sx=1-6=-5
Sy=1-3=-2
[BC]=(-5^2)+(-2^2)- под корнем
[BC]=5,3
3)l=[AB]+[BC]=12,4
4)AC:
Sx=1-0,5=0,5
Sy=1-7,5=-6,5
[AC]=(0,5^2)+(-6,5^2)- под корнем
[AC]=(перемещение)
5)l=12,4
S=6,5

№ 2 проекция вектора на ось

Sa: Sx=x-x0=5,5-1.5=4
     Sy=y-y0=2-1=1
|Sc|=√Sx2+Sy2 = √16+1=√17= 4,1

Sb: Sx=x-x0=4,5-7=-2,5
      Sy=y-y0=6,5-2=4,5
|Sa|= √Sx2+Sy2 = √6,25+20,25= 26,5




Sс: Sx=x-x0=3-1,5= 1,5
       Sy=y-y0=6,5-1=5,5
|Sb|=√Sx2+Sy2 = √2,25+30,25=32,5

моё задание